2 Square Root Of 16

Number whose square is a given number

Notation for the (principal) foursquare root of 10.

For example, √25 = v, since 25 = 5 ⋅ v, or 5² (five squared).

In mathematics, a foursquare root of a number x is a number y such that y ² = x ; in other words, a number y whose square (the upshot of multiplying the number by itself, or y  ⋅ y ) is 10 .^[one] For instance, iv and −4 are square roots of 16, considering 4² = (−4)^two = 16.

Every nonnegative existent number x has a unique nonnegative foursquare root, chosen the principal square root, which is denoted by ${\displaystyle {\sqrt {x}},}$ where the symbol ${\displaystyle {\sqrt {~^{~}}}}$ is chosen the radical sign ^[2] or radix. For example, to express the fact that the principal square root of 9 is iii, nosotros write ${\displaystyle {\sqrt {9}}=3}$ . The term (or number) whose foursquare root is existence considered is known equally the radicand. The radicand is the number or expression underneath the radical sign, in this case 9. For nonnegative 10 , the primary square root tin besides exist written in exponent note, as x ^i/2 .

Every positive number x has two square roots: ${\displaystyle {\sqrt {ten}},}$ which is positive, and ${\displaystyle -{\sqrt {x}},}$ which is negative. The two roots can be written more than concisely using the ± sign as ${\displaystyle \pm {\sqrt {10}}}$ . Although the principal foursquare root of a positive number is only one of its ii square roots, the designation "the square root" is oft used to refer to the main square root.^{[3] [4]}

Square roots of negative numbers tin exist discussed inside the framework of complex numbers. More by and large, square roots can be considered in any context in which a notion of the "square" of a mathematical object is divers. These include function spaces and foursquare matrices, amid other mathematical structures.

History

The Yale Babylonian Drove YBC 7289 clay tablet was created betwixt 1800 BC and 1600 BC, showing ${\displaystyle {\sqrt {ii}}}$ and ${\textstyle {\frac {\sqrt {2}}{2}}={\frac {1}{\sqrt {2}}}}$ respectively every bit 1;24,51,ten and 0;42,25,35 base threescore numbers on a foursquare crossed by two diagonals.^[5] (i;24,51,10) base sixty corresponds to 1.41421296, which is a correct value to five decimal points (1.41421356...).

The Rhind Mathematical Papyrus is a re-create from 1650 BC of an earlier Berlin Papyrus and other texts – possibly the Kahun Papyrus – that shows how the Egyptians extracted square roots by an changed proportion method.^{[half dozen]}

In Aboriginal Bharat, the knowledge of theoretical and applied aspects of square and square root was at least every bit old equally the Sulba Sutras, dated around 800–500 BC (possibly much earlier).^{[ citation needed ]} A method for finding very good approximations to the square roots of ii and 3 are given in the Baudhayana Sulba Sutra.^[7] Aryabhata, in the Aryabhatiya (department 2.iv), has given a method for finding the foursquare root of numbers having many digits.

Information technology was known to the ancient Greeks that square roots of positive integers that are not perfect squares are ever irrational numbers: numbers not expressible as a ratio of two integers (that is, they cannot exist written exactly every bit ${\textstyle {\frac {m}{north}}}$ , where thousand and n are integers). This is the theorem Euclid X, 9, almost certainly due to Theaetetus dating back to circa 380 BC.^[8] The item case of the square root of 2 is assumed to engagement back before to the Pythagoreans, and is traditionally attributed to Hippasus.^{[ citation needed ]} It is exactly the length of the diagonal of a square with side length 1.

In the Chinese mathematical work Writings on Reckoning, written between 202 BC and 186 BC during the early Han Dynasty, the square root is approximated by using an "excess and deficiency" method, which says to "...combine the excess and deficiency every bit the divisor; (taking) the deficiency numerator multiplied by the excess denominator and the excess numerator times the deficiency denominator, combine them equally the dividend."^[9]

A symbol for square roots, written as an elaborate R, was invented by Regiomontanus (1436–1476). An R was also used for radix to indicate square roots in Gerolamo Cardano'due south Ars Magna.^[ten]

According to historian of mathematics D.E. Smith, Aryabhata's method for finding the square root was showtime introduced in Europe by Cataneo—in 1546.

According to Jeffrey A. Oaks, Arabs used the letter of the alphabet jīm/ĝīm ( ج ), the starting time letter of the word " جذر " (variously transliterated every bit jaḏr, jiḏr, ǧaḏr or ǧiḏr, "root"), placed in its initial form ( ﺟ ) over a number to indicate its foursquare root. The letter jīm resembles the present square root shape. Its usage goes as far every bit the end of the twelfth century in the works of the Moroccan mathematician Ibn al-Yasamin.^[11]

The symbol "√" for the square root was showtime used in impress in 1525, in Christoph Rudolff'due south Coss.^[12]

Properties and uses

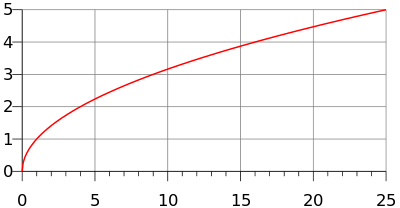
The graph of the function f(x) = √10, made upwards of half a parabola with a vertical directrix

The chief square root function ${\displaystyle f(10)={\sqrt {x}}}$ (usually just referred to equally the "square root role") is a function that maps the fix of nonnegative real numbers onto itself. In geometrical terms, the square root role maps the expanse of a square to its side length.

The square root of x is rational if and only if x is a rational number that tin be represented as a ratio of two perfect squares. (Run across square root of 2 for proofs that this is an irrational number, and quadratic irrational for a proof for all non-square natural numbers.) The foursquare root part maps rational numbers into algebraic numbers, the latter being a superset of the rational numbers).

For all real numbers x,

${\displaystyle {\sqrt {10^{2}}}=\left|x\right|={\brainstorm{cases}10,&{\mbox{if }}x\geq 0\\-x,&{\mbox{if }}x<0.\end{cases}}}$ (see absolute value)

For all nonnegative real numbers 10 and y,

${\displaystyle {\sqrt {xy}}={\sqrt {x}}{\sqrt {y}}}$

and

${\displaystyle {\sqrt {x}}=x^{1/2}.}$

The square root part is continuous for all nonnegative 10, and differentiable for all positive x. If f denotes the square root office, whose derivative is given by:

${\displaystyle f'(x)={\frac {1}{2{\sqrt {x}}}}.}$

The Taylor series of ${\displaystyle {\sqrt {1+ten}}}$ about x = 0 converges for | 10 | ≤ 1, and is given by

${\displaystyle {\sqrt {i+x}}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n)!}{(one-2n)(n!)^{two}(4^{n})}}ten^{n}=one+{\frac {1}{2}}x-{\frac {1}{8}}x^{ii}+{\frac {1}{xvi}}x^{3}-{\frac {5}{128}}x^{iv}+\cdots ,}$

The square root of a nonnegative number is used in the definition of Euclidean norm (and distance), besides as in generalizations such as Hilbert spaces. It defines an important concept of standard deviation used in probability theory and statistics. It has a major utilize in the formula for roots of a quadratic equation; quadratic fields and rings of quadratic integers, which are based on square roots, are of import in algebra and take uses in geometry. Square roots frequently appear in mathematical formulas elsewhere, equally well every bit in many concrete laws.

Square roots of positive integers

A positive number has two square roots, 1 positive, and ane negative, which are opposite to each other. When talking of the square root of a positive integer, it is usually the positive foursquare root that is meant.

The square roots of an integer are algebraic integers—more specifically quadratic integers.

The square root of a positive integer is the product of the roots of its prime number factors, because the foursquare root of a production is the product of the square roots of the factors. Since ${\displaystyle {\sqrt {p^{2k}}}=p^{k},}$ only roots of those primes having an odd power in the factorization are necessary. More precisely, the square root of a prime factorization is

${\displaystyle {\sqrt {p_{1}^{2e_{1}+i}\cdots p_{thousand}^{2e_{k}+1}p_{m+i}^{2e_{g+1}}\dots p_{north}^{2e_{north}}}}=p_{i}^{e_{1}}\dots p_{northward}^{e_{n}}{\sqrt {p_{1}\dots p_{k}}}.}$

As decimal expansions

The square roots of the perfect squares (e.g., 0, 1, 4, ix, 16) are integers. In all other cases, the square roots of positive integers are irrational numbers, and hence have not-repeating decimals in their decimal representations. Decimal approximations of the square roots of the first few natural numbers are given in the following table.

due north	${\displaystyle {\sqrt {n}},}$ truncated to 50 decimal places
0	0
1	1
2	i.41421356237309504880 1688724209 6980785696 7187537694
iii	1.73205080756887729352 7446341505 8723669428 0525381038
4	ii
5	ii.23606797749978969640 9173668731 2762354406 1835961152
6	ii.44948974278317809819 7284074705 8913919659 4748065667
7	two.64575131106459059050 1615753639 2604257102 5918308245
viii	2.82842712474619009760 3377448419 3961571393 4375075389
9	3
ten	3.16227766016837933199 8893544432 7185337195 5513932521

Every bit expansions in other numeral systems

As with before, the square roots of the perfect squares (e.k., 0, one, four, ix, 16) are integers. In all other cases, the square roots of positive integers are irrational numbers, and therefore have non-repeating digits in whatever standard positional annotation system.

The foursquare roots of small integers are used in both the SHA-i and SHA-two hash function designs to provide naught upwards my sleeve numbers.

As periodic connected fractions

One of the nigh intriguing results from the study of irrational numbers equally continued fractions was obtained by Joseph Louis Lagrange c. 1780. Lagrange found that the representation of the square root of any non-square positive integer as a continued fraction is periodic. That is, a sure blueprint of fractional denominators repeats indefinitely in the continued fraction. In a sense these foursquare roots are the very simplest irrational numbers, because they can be represented with a uncomplicated repeating pattern of integers.

${\displaystyle {\sqrt {two}}}$	= [1; ii, ii, ...]
${\displaystyle {\sqrt {3}}}$	= [one; one, 2, one, two, ...]
${\displaystyle {\sqrt {4}}}$	= [2]
${\displaystyle {\sqrt {five}}}$	= [two; iv, four, ...]
${\displaystyle {\sqrt {6}}}$	= [2; 2, iv, 2, 4, ...]
${\displaystyle {\sqrt {7}}}$	= [ii; i, one, 1, 4, 1, 1, 1, 4, ...]
${\displaystyle {\sqrt {8}}}$	= [2; one, 4, 1, iv, ...]
${\displaystyle {\sqrt {9}}}$	= [3]
${\displaystyle {\sqrt {ten}}}$	= [3; six, 6, ...]
${\displaystyle {\sqrt {xi}}}$	= [3; 3, 6, 3, half-dozen, ...]
${\displaystyle {\sqrt {12}}}$	= [3; 2, vi, 2, 6, ...]
${\displaystyle {\sqrt {13}}}$	= [three; ane, 1, one, 1, 6, one, 1, 1, 1, vi, ...]
${\displaystyle {\sqrt {fourteen}}}$	= [3; ane, 2, 1, 6, one, two, 1, 6, ...]
${\displaystyle {\sqrt {xv}}}$	= [iii; 1, 6, 1, 6, ...]
${\displaystyle {\sqrt {16}}}$	= [4]
${\displaystyle {\sqrt {17}}}$	= [4; 8, viii, ...]
${\displaystyle {\sqrt {eighteen}}}$	= [4; iv, 8, four, 8, ...]
${\displaystyle {\sqrt {19}}}$	= [four; ii, i, 3, 1, 2, eight, ii, 1, three, 1, 2, 8, ...]
${\displaystyle {\sqrt {20}}}$	= [four; ii, viii, 2, viii, ...]

The foursquare bracket notation used above is a short form for a continued fraction. Written in the more suggestive algebraic grade, the simple continued fraction for the foursquare root of 11, [3; 3, 6, 3, 6, ...], looks similar this:

${\displaystyle {\sqrt {11}}=iii+{\cfrac {i}{3+{\cfrac {ane}{6+{\cfrac {1}{3+{\cfrac {one}{6+{\cfrac {i}{3+\ddots }}}}}}}}}}}$

where the ii-digit pattern {three, 6} repeats over and over again in the partial denominators. Since xi = iiiⁱⁱ + 2, the above is also identical to the post-obit generalized continued fractions:

${\displaystyle {\sqrt {11}}=3+{\cfrac {ii}{half dozen+{\cfrac {2}{6+{\cfrac {2}{six+{\cfrac {2}{half dozen+{\cfrac {2}{6+\ddots }}}}}}}}}}=3+{\cfrac {half dozen}{20-1-{\cfrac {one}{20-{\cfrac {1}{20-{\cfrac {one}{20-{\cfrac {ane}{20-\ddots }}}}}}}}}}.}$

Computation

Square roots of positive numbers are not in general rational numbers, and and then cannot be written as a terminating or recurring decimal expression. Therefore in full general any attempt to compute a square root expressed in decimal form can simply yield an approximation, though a sequence of increasingly accurate approximations tin can be obtained.

Most pocket calculators have a square root key. Computer spreadsheets and other software are also frequently used to calculate square roots. Pocket calculators typically implement efficient routines, such as the Newton'south method (frequently with an initial estimate of 1), to compute the square root of a positive existent number.^{[thirteen] [14]} When computing square roots with logarithm tables or slide rules, i tin can exploit the identities

${\displaystyle {\sqrt {a}}=e^{(\ln a)/two}=ten^{(\log _{ten}a)/2},}$

where ln and log _ten are the natural and base-10 logarithms.

By trial-and-error,^[xv] one can square an estimate for ${\displaystyle {\sqrt {a}}}$ and raise or lower the estimate until information technology agrees to sufficient accuracy. For this technique it is prudent to apply the identity

${\displaystyle (x+c)^{2}=x^{ii}+2xc+c^{two},}$

as information technology allows ane to arrange the estimate x by some corporeality c and measure out the square of the adjustment in terms of the original approximate and its foursquare. Furthermore, (x + c)^two ≈ x ^two + 2xc when c is close to 0, because the tangent line to the graph of x ² + 2xc + c ² at c = 0, as a function of c alone, is y = 2xc + 10 ⁱⁱ. Thus, small adjustments to x can exist planned out by setting 2xc to a, or c = a/(210).

The about common iterative method of square root calculation by paw is known as the "Babylonian method" or "Heron's method" afterwards the first-century Greek philosopher Heron of Alexandria, who kickoff described it.^[sixteen] The method uses the same iterative scheme as the Newton–Raphson method yields when applied to the function y = f(10) = x ² − a, using the fact that its slope at any indicate is dy/dx = f′ (x) = 2x, but predates it by many centuries.^[17] The algorithm is to repeat a uncomplicated calculation that results in a number closer to the bodily square root each time it is repeated with its upshot equally the new input. The motivation is that if x is an overestimate to the square root of a nonnegative real number a then a/x will be an underestimate then the boilerplate of these two numbers is a better approximation than either of them. However, the inequality of arithmetic and geometric means shows this average is always an overestimate of the square root (as noted below), and then it tin serve as a new overestimate with which to repeat the process, which converges equally a consequence of the successive overestimates and underestimates being closer to each other after each iteration. To find x:

1. Start with an arbitrary positive kickoff value x. The closer to the square root of a, the fewer the iterations that volition be needed to achieve the desired precision.
2. Supplant x by the average (ten + a/10) / ii between x and a/x.
3. Repeat from pace 2, using this average as the new value of x.

That is, if an arbitrary approximate for ${\displaystyle {\sqrt {a}}}$ is ten ₀, and ten _{northward + 1} = (x_n + a/x_n ) / 2, then each x_n is an approximation of ${\displaystyle {\sqrt {a}}}$ which is better for big n than for minor n. If a is positive, the convergence is quadratic, which ways that in approaching the limit, the number of correct digits roughly doubles in each adjacent iteration. If a = 0, the convergence is only linear.

Using the identity

${\displaystyle {\sqrt {a}}=2^{-north}{\sqrt {4^{due north}a}},}$

the computation of the square root of a positive number can be reduced to that of a number in the range [one,four). This simplifies finding a first value for the iterative method that is close to the square root, for which a polynomial or piecewise-linear approximation can be used.

The time complexity for computing a foursquare root with n digits of precision is equivalent to that of multiplying ii n-digit numbers.

Another useful method for calculating the square root is the shifting nth root algorithm, practical for north = 2.

The name of the square root part varies from programming linguistic communication to programming language, with sqrt ^[18] (often pronounced "squirt" ^[19]) beingness mutual, used in C, C++, and derived languages like JavaScript, PHP, and Python.

Square roots of negative and circuitous numbers

First leafage of the complex square root

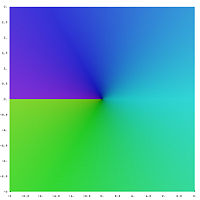
Second leaf of the complex foursquare root

Using the Riemann surface of the foursquare root, information technology is shown how the two leaves fit together

The square of any positive or negative number is positive, and the square of 0 is 0. Therefore, no negative number can have a real square root. However, it is possible to piece of work with a more inclusive ready of numbers, called the complex numbers, that does contain solutions to the square root of a negative number. This is done by introducing a new number, denoted past i (sometimes j, especially in the context of electricity where "i" traditionally represents electric electric current) and chosen the imaginary unit, which is divers such that i ² = −1. Using this notation, nosotros can think of i as the square root of −1, only we also accept (−i)² = i ⁱⁱ = −1 and and so −i is also a foursquare root of −1. By convention, the main foursquare root of −1 is i, or more by and large, if x is whatever nonnegative number, so the principal square root of −10 is

${\displaystyle {\sqrt {-x}}=i{\sqrt {ten}}.}$

The right side (as well as its negative) is indeed a square root of −ten, since

${\displaystyle (i{\sqrt {x}})^{two}=i^{two}({\sqrt {10}})^{2}=(-ane)x=-x.}$

For every not-zippo complex number z at that place exist precisely two numbers w such that westward ⁱⁱ = z : the principal foursquare root of z (defined beneath), and its negative.

Master square root of a complex number

Geometric representation of the second to sixth roots of a circuitous number z, in polar form re ^iφ where r = |z | and φ = arg z . If z is existent, φ = 0 or π . Principal roots are shown in black.

To observe a definition for the square root that allows u.s.a. to consistently choose a unmarried value, chosen the principal value, we start past observing that whatever circuitous number ${\displaystyle ten+iy}$ tin be viewed as a bespeak in the airplane, ${\displaystyle (x,y),}$ expressed using Cartesian coordinates. The same point may be reinterpreted using polar coordinates as the pair ${\displaystyle (r,\varphi ),}$ where ${\displaystyle r\geq 0}$ is the distance of the point from the origin, and ${\displaystyle \varphi }$ is the bending that the line from the origin to the point makes with the positive existent ( ${\displaystyle x}$ ) axis. In complex analysis, the location of this point is conventionally written ${\displaystyle re^{i\varphi }.}$ If

$${\displaystyle z=re^{i\varphi }{\text{ with }}-\pi <\varphi \leq \pi ,}$$

then the primary square root of ${\displaystyle z}$ is defined to be the post-obit:

$${\displaystyle {\sqrt {z}}={\sqrt {r}}e^{i\varphi /2}.}$$

The main foursquare root office is thus defined using the nonpositive real axis as a co-operative cut. If ${\displaystyle z}$ is a non-negative real number (which happens if and only if ${\displaystyle \varphi =0}$ ) then the principal foursquare root of ${\displaystyle z}$ is ${\displaystyle {\sqrt {r}}eastward^{i(0)/2}={\sqrt {r}};}$ in other words, the principal square root of a non-negative real number is merely the usual non-negative square root. Information technology is important that ${\displaystyle -\pi <\varphi \leq \pi }$ because if, for example, ${\displaystyle z=-2i}$ (then ${\displaystyle \varphi =-\pi /2}$ ) and so the principal foursquare root is

$${\displaystyle {\sqrt {-2i}}={\sqrt {2e^{i\varphi }}}={\sqrt {2}}e^{i\varphi /2}={\sqrt {two}}east^{i(-\pi /iv)}=ane-i}$$

just using ${\displaystyle {\tilde {\varphi }}:=\varphi +2\pi =three\pi /two}$ would instead produce the other square root ${\displaystyle {\sqrt {2}}east^{i{\tilde {\varphi }}/2}={\sqrt {2}}e^{i(iii\pi /four)}=-i+i=-{\sqrt {-2i}}.}$

The main foursquare root function is holomorphic everywhere except on the set of non-positive real numbers (on strictly negative reals it is non even continuous). The to a higher place Taylor series for ${\displaystyle {\sqrt {ane+x}}}$ remains valid for complex numbers ${\displaystyle x}$ with ${\displaystyle |x|<one.}$

The higher up can also be expressed in terms of trigonometric functions:

$${\displaystyle {\sqrt {r\left(\cos \varphi +i\sin \varphi \correct)}}={\sqrt {r}}\left(\cos {\frac {\varphi }{two}}+i\sin {\frac {\varphi }{2}}\right).}$$

Algebraic formula

When the number is expressed using its real and imaginary parts, the following formula tin can be used for the main square root:^{[20] [21]}

${\displaystyle {\sqrt {ten+iy}}={\sqrt {\frac {{\sqrt {x^{2}+y^{2}}}+x}{2}}}+i\operatorname {sgn}(y){\sqrt {\frac {{\sqrt {ten^{2}+y^{ii}}}-x}{ii}}},}$

where sgn(y) is the sign of y (except that, hither, sgn(0) = i). In item, the imaginary parts of the original number and the principal value of its square root have the same sign. The existent part of the principal value of the square root is always nonnegative.

For example, the principal square roots of ±i are given by:

${\displaystyle {\begin{aligned}{\sqrt {i}}&={\frac {ane}{\sqrt {2}}}+i{\frac {1}{\sqrt {two}}}={\frac {\sqrt {2}}{two}}(ane+i),\\{\sqrt {-i}}&={\frac {i}{\sqrt {2}}}-i{\frac {1}{\sqrt {2}}}={\frac {\sqrt {two}}{2}}(1-i).\cease{aligned}}}$

Notes

In the following, the circuitous z and w may exist expressed every bit:

where ${\displaystyle -\pi <\theta _{z}\leq \pi }$ and ${\displaystyle -\pi <\theta _{w}\leq \pi }$ .

Because of the discontinuous nature of the foursquare root office in the complex plane, the following laws are non true in general.

A similar problem appears with other complex functions with co-operative cuts, e.g., the complex logarithm and the relations logz + logwestward = log(zw) or log(z ^*) = log(z)^* which are not true in general.

Wrongly bold one of these laws underlies several faulty "proofs", for instance the following 1 showing that −one = 1:

${\displaystyle {\begin{aligned}-i&=i\cdot i\\&={\sqrt {-i}}\cdot {\sqrt {-1}}\\&={\sqrt {\left(-1\right)\cdot \left(-1\right)}}\\&={\sqrt {1}}\\&=i.\cease{aligned}}}$

The 3rd equality cannot be justified (encounter invalid proof).^{[22] : Affiliate Six Some fallacies in algebra and trigonometry, Section I The fallacies, Subsection two The fallacy that +1 = -i} It can exist made to hold by changing the meaning of √ then that this no longer represents the main square root (meet to a higher place) just selects a branch for the square root that contains ${\displaystyle {\sqrt {1}}\cdot {\sqrt {-i}}.}$ The left-hand side becomes either

${\displaystyle {\sqrt {-1}}\cdot {\sqrt {-i}}=i\cdot i=-1}$

if the branch includes +i or

${\displaystyle {\sqrt {-1}}\cdot {\sqrt {-1}}=(-i)\cdot (-i)=-1}$

if the co-operative includes −i, while the right-paw side becomes

${\displaystyle {\sqrt {\left(-1\correct)\cdot \left(-1\right)}}={\sqrt {1}}=-one,}$

where the last equality, ${\displaystyle {\sqrt {ane}}=-ane,}$ is a consequence of the choice of branch in the redefinition of √.

Nth roots and polynomial roots

The definition of a square root of ${\displaystyle x}$ as a number ${\displaystyle y}$ such that ${\displaystyle y^{2}=x}$ has been generalized in the following way.

A cube root of ${\displaystyle x}$ is a number ${\displaystyle y}$ such that ${\displaystyle y^{3}=x}$ ; it is denoted ${\displaystyle {\sqrt[{3}]{ten}}.}$

If n is an integer greater than two, a due northth root of ${\displaystyle x}$ is a number ${\displaystyle y}$ such that ${\displaystyle y^{due north}=x}$ ; it is denoted ${\displaystyle {\sqrt[{n}]{x}}.}$

Given whatsoever polynomial p , a root of p is a number y such that p(y) = 0. For case, the due northth roots of x are the roots of the polynomial (in y) ${\displaystyle y^{n}-x.}$

Abel–Ruffini theorem states that, in general, the roots of a polynomial of degree five or higher cannot be expressed in terms of nth roots.

Square roots of matrices and operators

If A is a positive-definite matrix or operator, so there exists precisely one positive definite matrix or operator B with B ² = A ; we and so define A ^1/2 = B . In general matrices may have multiple square roots or even an infinitude of them. For case, the 2 × two identity matrix has an infinity of square roots,^[23] though only one of them is positive definite.

In integral domains, including fields

Each element of an integral domain has no more than than 2 square roots. The divergence of two squares identity u ² − v ^two = (u − v)(u + 5) is proved using the commutativity of multiplication. If u and v are square roots of the same element, and then u ² − 5 ² = 0. Considering there are no zero divisors this implies u = v or u + v = 0, where the latter means that 2 roots are additive inverses of each other. In other words if an element a square root u of an element a exists, then the only square roots of a are u and −u. The merely square root of 0 in an integral domain is 0 itself.

In a field of characteristic 2, an element either has one square root or does not have whatsoever at all, because each chemical element is its own additive inverse, so that −u = u . If the field is finite of feature ii then every element has a unique square root. In a field of any other characteristic, any non-zero chemical element either has two square roots, as explained higher up, or does not have whatever.

Given an odd prime number p, let q = p ^e for some positive integer e. A non-cipher element of the field F _q with q elements is a quadratic rest if it has a foursquare root in F _q . Otherwise, information technology is a quadratic not-residue. At that place are (q − 1)/2 quadratic residues and (q − 1)/2 quadratic non-residues; nothing is not counted in either class. The quadratic residues course a group under multiplication. The properties of quadratic residues are widely used in number theory.

In rings in full general

Unlike in an integral domain, a foursquare root in an arbitrary (unital) ring need not exist unique upwardly to sign. For example, in the band ${\displaystyle \mathbb {Z} /8\mathbb {Z} }$ of integers modulo 8 (which is commutative, just has cipher divisors), the element ane has four singled-out square roots: ±1 and ±three.

Another case is provided by the ring of quaternions ${\displaystyle \mathbb {H} ,}$ which has no naught divisors, just is not commutative. Here, the element −1 has infinitely many foursquare roots, including ±i , ±j , and ±thou . In fact, the fix of foursquare roots of −1 is exactly

${\displaystyle \{ai+bj+ck\mid a^{2}+b^{two}+c^{2}=i\}.}$

A square root of 0 is either 0 or a naught divisor. Thus in rings where zero divisors practise non exist, information technology is uniquely 0. Notwithstanding, rings with nil divisors may have multiple foursquare roots of 0. For example, in ${\displaystyle \mathbb {Z} /n^{2}\mathbb {Z} ,}$ any multiple of n is a foursquare root of 0.

Geometric construction of the foursquare root

Constructing the length ${\displaystyle 10={\sqrt {a}}}$ , given the ${\displaystyle a}$ and the unit of measurement length

The square root of a positive number is usually defined every bit the side length of a foursquare with the expanse equal to the given number. Merely the square shape is not necessary for information technology: if 1 of two similar planar Euclidean objects has the area a times greater than another, then the ratio of their linear sizes is ${\displaystyle {\sqrt {a}}}$ .

A square root can exist constructed with a compass and straightedge. In his Elements, Euclid (fl. 300 BC) gave the structure of the geometric mean of ii quantities in two different places: Suggestion II.xiv and Proposition VI.13. Since the geometric hateful of a and b is ${\displaystyle {\sqrt {ab}}}$ , one can construct ${\displaystyle {\sqrt {a}}}$ just by taking b = 1.

The construction is too given by Descartes in his La Géométrie, run into figure 2 on page two. However, Descartes fabricated no claim to originality and his audience would take been quite familiar with Euclid.

Euclid's second proof in Book VI depends on the theory of like triangles. Let AHB be a line segment of length a + b with AH = a and HB = b . Construct the circle with AB as diameter and permit C be one of the 2 intersections of the perpendicular chord at H with the circle and announce the length CH as h. So, using Thales' theorem and, as in the proof of Pythagoras' theorem by similar triangles, triangle AHC is like to triangle CHB (as indeed both are to triangle ACB, though we don't need that, but it is the essence of the proof of Pythagoras' theorem) so that AH:CH is as HC:HB, i.eastward. a/h = h/b , from which we conclude by cross-multiplication that h ² = ab , and finally that ${\displaystyle h={\sqrt {ab}}}$ . When marking the midpoint O of the line segment AB and cartoon the radius OC of length (a + b)/2, then conspicuously OC > CH, i.east. ${\textstyle {\frac {a+b}{2}}\geq {\sqrt {ab}}}$ (with equality if and just if a = b ), which is the arithmetic–geometric mean inequality for two variables and, as noted above, is the basis of the Ancient Greek understanding of "Heron's method".

Another method of geometric construction uses right triangles and induction: ${\displaystyle {\sqrt {i}}}$ can exist constructed, and once ${\displaystyle {\sqrt {10}}}$ has been constructed, the correct triangle with legs 1 and ${\displaystyle {\sqrt {ten}}}$ has a hypotenuse of ${\displaystyle {\sqrt {ten+1}}}$ . Constructing successive square roots in this style yields the Spiral of Theodorus depicted in a higher place.

See also

• Apotome (mathematics)
• Cube root
• Functional foursquare root
• Integer foursquare root
• Nested radical
• Nth root
• Root of unity
• Solving quadratic equations with continued fractions
• Foursquare root principle
• Quantum gate § Foursquare root of Not gate (√Non)

Notes

1. ^ Gel'fand, p. 120 Archived 2016-09-02 at the Wayback Machine
2. ^ "Squares and Square Roots". www.mathsisfun.com . Retrieved 2020-08-28 .
3. ^ Zill, Dennis 1000.; Shanahan, Patrick (2008). A First Class in Circuitous Analysis With Applications (2nd ed.). Jones & Bartlett Learning. p. 78. ISBN978-0-7637-5772-4. Archived from the original on 2016-09-01. Extract of page 78 Archived 2016-09-01 at the Wayback Machine
4. ^ Weisstein, Eric W. "Square Root". mathworld.wolfram.com . Retrieved 2020-08-28 .
5. ^ "Analysis of YBC 7289". ubc.ca . Retrieved 19 January 2015.
6. ^ Anglin, Westward.S. (1994). Mathematics: A Concise History and Philosophy. New York: Springer-Verlag.
7. ^ Joseph, ch.8.
8. ^ Heath, Sir Thomas L. (1908). The Thirteen Books of The Elements, Vol. three. Cambridge University Press. p. three.
9. ^ Dauben (2007), p. 210.
10. ^ "The Development of Algebra - 2". maths.org. Archived from the original on 24 November 2014. Retrieved 19 January 2015.
11. ^ * Oaks, Jeffrey A. (2012). Algebraic Symbolism in Medieval Arabic Algebra (PDF) (Thesis). Philosophica. p. 36. Archived (PDF) from the original on 2016-12-03.
12. ^ Manguel, Alberto (2006). "Done on newspaper: the dual nature of numbers and the page". The Life of Numbers. ISBN84-86882-14-1.
13. ^ Parkhurst, David F. (2006). Introduction to Applied Mathematics for Environmental Science . Springer. pp. 241. ISBN9780387342283.
14. ^ Solow, Anita E. (1993). Learning by Discovery: A Lab Manual for Calculus. Cambridge University Press. pp. 48. ISBN9780883850831.
15. ^ Aitken, Mike; Broadhurst, Nib; Hladky, Stephen (2009). Mathematics for Biological Scientists. Garland Science. p. 41. ISBN978-i-136-84393-8. Archived from the original on 2017-03-01. Extract of page 41 Archived 2017-03-01 at the Wayback Motorcar
16. ^ Heath, Sir Thomas L. (1921). A History of Greek Mathematics, Vol. two. Oxford: Clarendon Press. pp. 323–324.
17. ^ Muller, Jean-Mic (2006). Unproblematic functions: algorithms and implementation. Springer. pp. 92–93. ISBN0-8176-4372-ix. , Chapter 5, p 92 Archived 2016-09-01 at the Wayback Machine
18. ^ "Function sqrt". CPlusPlus.com. The C++ Resources Network. 2016. Archived from the original on November 22, 2012. Retrieved June 24, 2016.
19. ^ Overland, Brian (2013). C++ for the Impatient. Addison-Wesley. p. 338. ISBN9780133257120. OCLC 850705706. Archived from the original on September i, 2016. Retrieved June 24, 2016.
20. ^ Abramowitz, Milton; Stegun, Irene A. (1964). Handbook of mathematical functions with formulas, graphs, and mathematical tables. Courier Dover Publications. p. 17. ISBN0-486-61272-4. Archived from the original on 2016-04-23. , Section 3.7.27, p. 17 Archived 2009-09-x at the Wayback Automobile
21. ^ Cooke, Roger (2008). Classical algebra: its nature, origins, and uses. John Wiley and Sons. p. 59. ISBN978-0-470-25952-8. Archived from the original on 2016-04-23.
22. ^ Maxwell, E. A. (1959). Fallacies in Mathematics. Cambridge University Press.
23. ^ Mitchell, Douglas W., "Using Pythagorean triples to generate square roots of I_two", Mathematical Gazette 87, November 2003, 499–500.

References

• Dauben, Joseph W. (2007). "Chinese Mathematics I". In Katz, Victor J. (ed.). The Mathematics of Egypt, Mesopotamia, China, India, and Islam. Princeton: Princeton University Press. ISBN978-0-691-11485-ix.
• Gel'fand, Izrael 1000.; Shen, Alexander (1993). Algebra (third ed.). Birkhäuser. p. 120. ISBN0-8176-3677-three.
• Joseph, George (2000). The Crest of the Peacock. Princeton: Princeton University Press. ISBN0-691-00659-viii.
• Smith, David (1958). History of Mathematics. Vol. 2. New York: Dover Publications. ISBN978-0-486-20430-7.
• Selin, Helaine (2008), Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures, Springer, Bibcode:2008ehst.volume.....Due south, ISBN978-1-4020-4559-2 .

External links

• Algorithms, implementations, and more – Paul Hsieh'southward square roots webpage
• How to manually notice a foursquare root
• AMS Featured Column, Galileo's Arithmetic by Tony Philips – includes a section on how Galileo institute square roots

2 Square Root Of 16,

Source: https://en.wikipedia.org/wiki/Square_root

Posted by: callahanwassaimmat44.blogspot.com

Share this post